Auteur/autrice : Éditorialiste e-FRAN

Catégories
Thèses

Conception d’un système tutoriel intelligent orienté stylet pour l’apprentissage de la géométrie basé sur une interprétation à la volée de la production manuscrite de figures

Omar KRICHEN

Niveaux

Collège

 

 

Public

Professeur·es de mathématiques au collège

 

 

Contact

Omar KRICHEN — Voir ses publications

Institut IRISA

Action/Projet associé(e)

ACTIF

Ressource(s) associée(s)

IntuiGEO

© Vidéo YouTube : Soutenance Thèse KRICHEN Omar
Ce résumé
Manuscrit de thèse

À quelles questions cette étude tente-t-elle de répondre ?

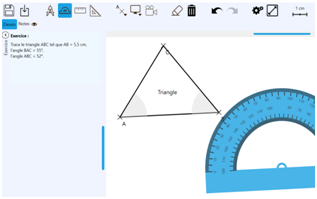
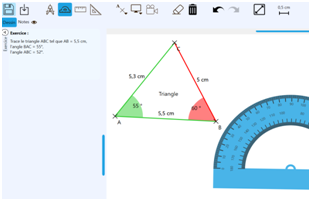
Ce travail de recherche, effectué dans le cadre du projet Actif, a consisté à concevoir un système tutoriel pour l’apprentissage de la géométrie au collège sur tablette stylet, nommé « IntuiGeo ». Cet outil a été développé au sein de l’équipe IntuiDoc de l’INSA Rennes, en collaboration avec le LP3C de l’université de Rennes 2. Ce tuteur simule l’approche traditionnelle papier/crayon, en permettant à l’élève de dessiner librement avec le stylet tout en manipulant avec ses doigts des outils virtuels (par exemple la règle dans la Figure 1).

Les enjeux pédagogiques sont les suivants : (1) garantir la transférabilité de l’apprentissage entre support numérique et support papier, (2) fournir des feedbacks personnalisés en immédiats pour stimuler l’apprentissage.

Photo montrant un élève utilisant le logiciel IntuiGeo sur tablette
Figure 1 – Simulation de l’approche traditionnelle IntuiGeo.

Pourquoi ces questions sont-elles pertinentes ?

Question 1 : Comment garantir la transférabilité de l’apprentissage ?
La plupart des outils de géométrie dynamique, tels que le populaire Geogebra (Bhagat et Chang, 2015), ou Cabri-Geometrie (Laborde, 2002), se caractérisent par une approche glisser-déposer (l’élève utilise des boutons et des menus pour placer et manipuler des objets dans l’interface). Cette approche s’éloigne de la construction traditionnelle de figures sur papier. Par conséquent, la connaissance acquise sur le logiciel pourrait être perdue lors du transfert du support numérique vers le papier. L’idée de notre travail est d’avoir les bénéfices du numérique tout en simulant l’approche papier-crayon pour que l’élève puisse naviguer entre les supports sans perdre ses acquis. Pour pouvoir interpréter et évaluer la validité du dessin libre de l’élève par rapport à une consigne, notre système reconnaît les tracés manuscrits de l’élève et les transforme en éléments géométriques. Pour pouvoir interagir en temps-réel avec l’utilisateur·rice, notamment pour générer des feedbacks immédiats, notre système doit non seulement reconnaître les tracés de l’élève, mais aussi les interpréter à la volée (au fil de la composition). Nous avons conçu un moteur de reconnaissance qui se base sur une grammaire visuelle capable d’interpréter les tracés manuscrits (Macé et Anquetil, 2009). Les détails concernant ce moteur sont fournis par Krichen et al. (2018).

Question 2 : Quel impact des feedbacks immédiats sur l’apprentissage ?
Deux modes de génération de feedbacks se distinguent : le premier est dit différé (c’est-à-dire, après la réalisation de l’exercice), et le second est dit immédiat (c’est-à-dire, au fil de la résolution). Chickering (1987) confirment la pertinence de ce deuxième type de feedbacks, estimant que pour avoir un impact sur la performance, le retour doit être immédiat. Le feedback correctif est une description des erreurs effectuées ([AB] doit être parallèle à [DC]), alors que le feedback de guidage est une indication sur les prochaines actions à réaliser (utilise le compas pour dessiner le point C).

Pour pouvoir générer des feedbacks de correction et de guidage personnalisés, le système doit modéliser la connaissance experte du domaine. Nous nous sommes inspirés de la littérature des systèmes tutoriels intelligents (Nkambou et al., 2010), pour concevoir un moteur de supervision qui remplit trois rôles principaux :

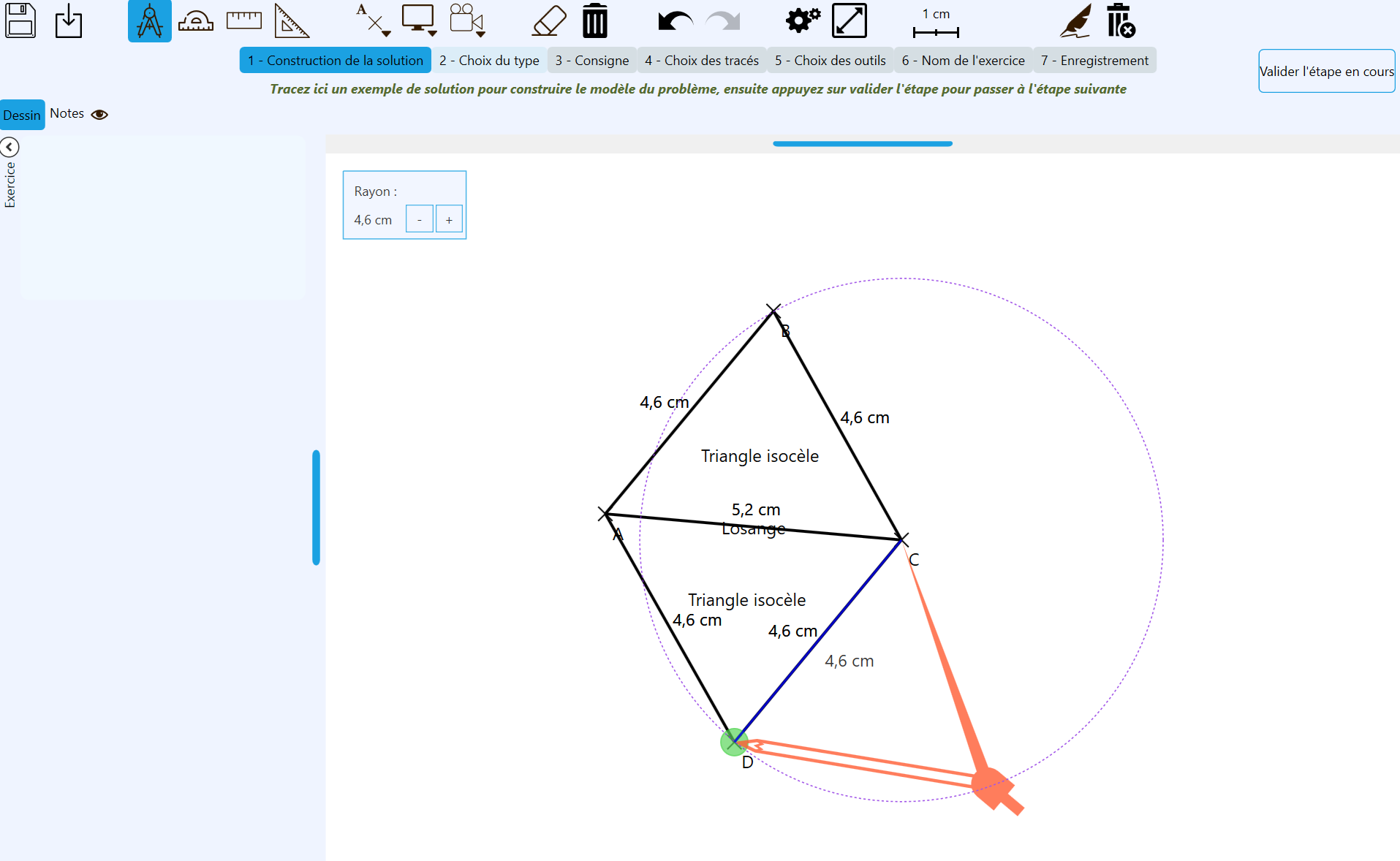
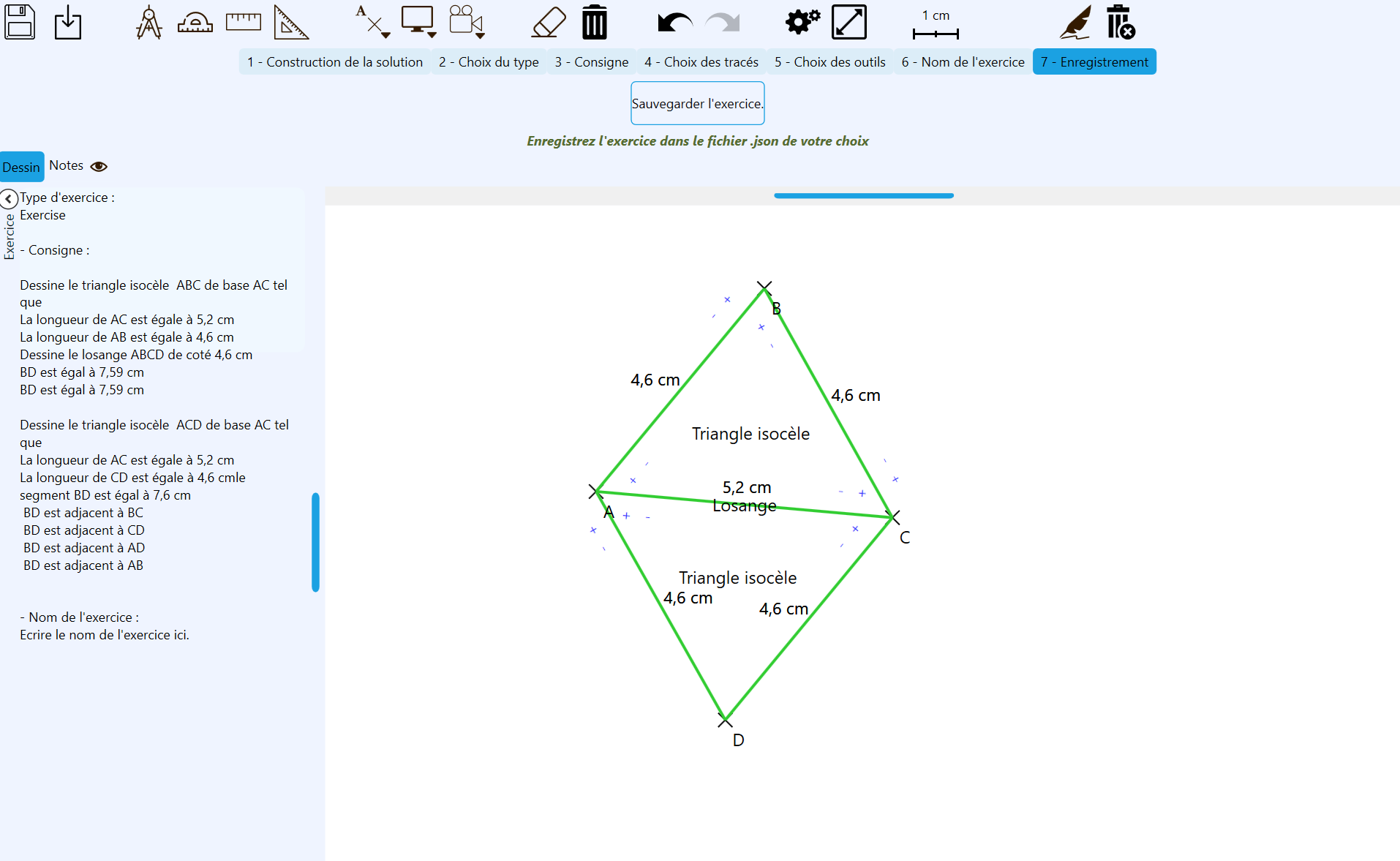
  • La génération automatique d’un problème de construction, à partir d’un exemple de solution dessiné par l’enseignant·e : module auteur.
    L’enseignant·e dessine la solution sur l’interface. Sa production est interprétée par le système et un modèle du problème, représenté par un graphe de connaissance (Yan et al., 2018), est généré.
    Ce graphe représente les éléments géométriques construits par l’enseignant·e, et les contraintes qui les lient. Ce graphe est la base de l’évaluation des actions de l’élève ;
  • La supervision en temps-réel du processus de résolution : module apprenant.
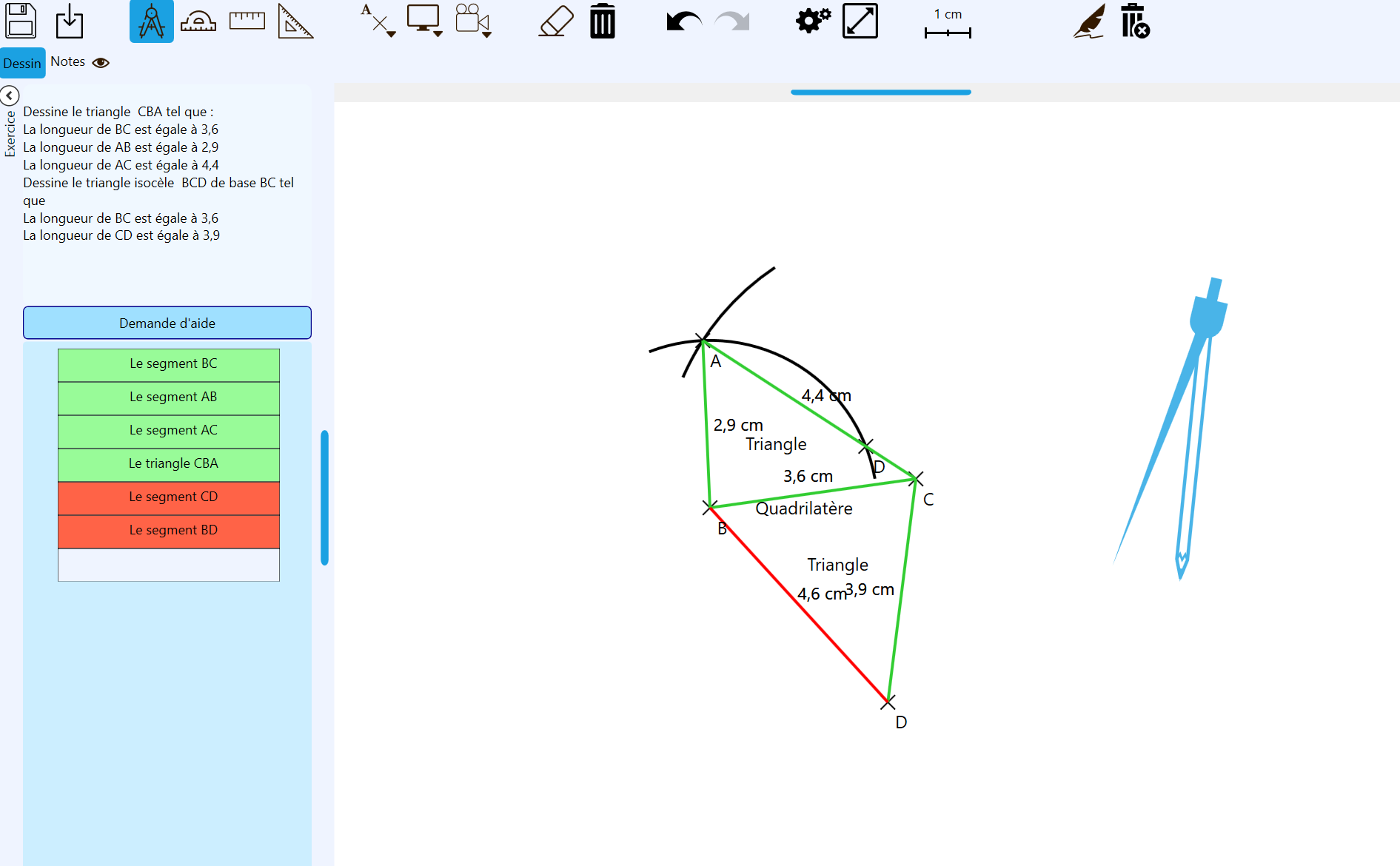
    Ce module est responsable de l’évaluation au « fil de l’eau » de la réalisation de l’élève. À chaque nouvelle action de l’élève, le tracé est reconnu et mis en correspondance avec le graphe de connaissance. Cela permet un suivi en temps-réel de l’élève et la génération de feedbacks de correction adaptés ;
  • La synthèse de stratégie pour la résolution d’un exercice : module expert.
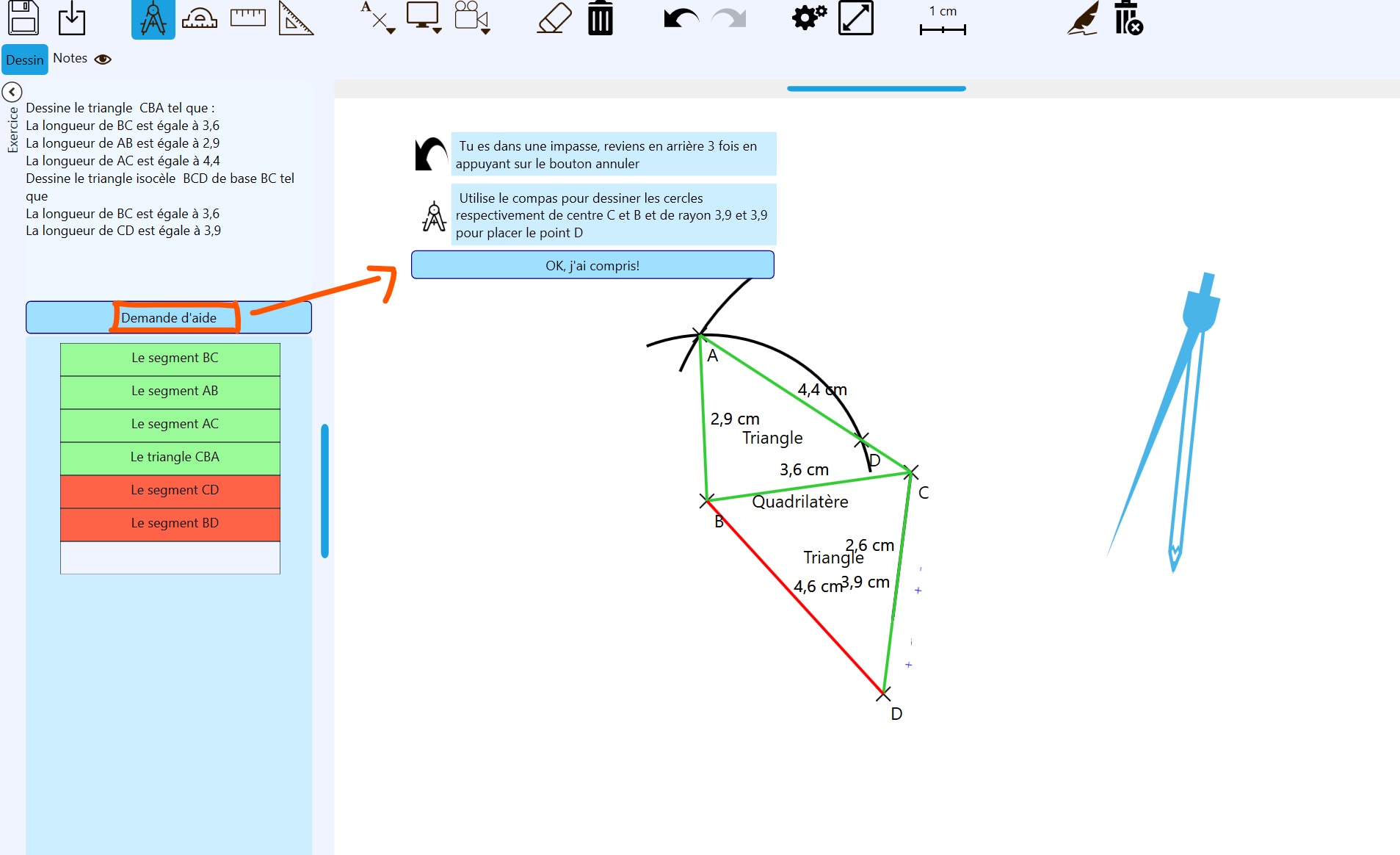
    Pour pouvoir superviser la réalisation de l’élève et l’aider en cas de blocage, le tuteur doit être capable de résoudre l’exercice. Pour ce faire, nous définissons un module expert, basé sur un environnement de planification (Ghallab et al., 2004). L’objectif pour ce module expert est de trouver, à partir de l’état de résolution de l’élève, une solution au problème qui sera traduite en feedbacks de guidage sur les prochaines actions à réaliser.

Plus de détails sur l’aspect tutoriel de ces trois modules sont fournis par Krichen et al. (2020).

Quelle méthodologie de recherche a-t-on utilisée ?

Des expérimentations en classe ont été conduites par nos collègues du LP3C/Loustic, expert·e·s en psychologie expérimentale et en science des usages. L’objectif de ces expérimentations est triple :

  1. Comparer la performance de l’élève relativement au support : traditionnel papier-crayon ou numérique tablette stylet ;
  2. Étudier l’effet du feedback de correction sur le taux de réussite de l’élève ;
  3. Évaluer la transférabilité de l’apprentissage du support numérique vers le support papier.

Ces expérimentations ont donc porté sur l’impact pédagogique de notre module apprenant, responsable de la génération de feedbacks correctifs immédiats. Les expérimentations relatives à l’évaluation du système tant sur l’aspect reconnaissance de formes, ou sur l’aspect tutoriel, davantage « techniques » car axées sur l’intelligence artificielle, ne sont pas présentées dans ce résumé mais peuvent être consultées dans (Krichen, 2020 ; Krichen et al., 2020 ; Krichen et al., 2018).

Protocole expérimental

Les participant·e·s sont des élèves de collège en classe de 5e, de l’académie de Rennes. Au total, 85 élèves ont participé à l’étude (39 filles et 46 garçons). Il·elle·s ont été affecté·e·s, de façon aléatoire, à l’un des trois groupes suivants :

  • Le groupe contrôle : réalisation de figures sur support papier (condition traditionnelle), composé de 27 élèves (Figure 2.a) ;
  • Le groupe IntuiGeo sans feedbacks : utilisation d’IntuiGeo comme éditeur de figures, composé de 28 élèves (Figure 2.b) ;
  • Le groupe IntuiGeo avec feedbacks : génération par le tuteur de feedbacks correctifs en temps-réel, composé de 30 élèves (Figure 2.c).

Pour le groupe IntuiGeo avec feedbacks, les segments et les angles se colorient automatiquement en vert si la mesure — longueur ou angle — est correcte, en rouge sinon (voir Figure 2.c).

L’intérêt du groupe IntuiGeo sans feedbacks est d’isoler l’effet du feedback de l’effet du support utilisé. Cette condition s’approche le plus de la condition traditionnelle, ce qui nous permet d’observer s’il y a un effet intrinsèque au support (la tablette) sur la performance des élèves.

Photo d'un élève du groupe contrôle qui réalise une activité. Description détaillée ci-dessous.
Figure 2.a – Illustration d’une activité réalisée dans le groupe contrôle.
Exemple d'activité réalisée dans le groupe IntuiGeo sans feedbacks. Description détaillée ci-dessous.
Figure 2.b – Illustration d’une activité réalisée dans le groupe expérimental IntuiGeo sans feedbacks.
Exemple d'activité réalisée dans le groupe IntuiGeo avec feedbacks. Description détaillée ci-dessous.
Figure 2.c – Illustration d’une activité réalisée dans le groupe expérimental IntuiGeo avec feedbacks.

Procédure d’évaluation des performances

Notre procédure d’évaluation était constituée de trois phases que nous détaillons dans les sous sections suivantes.

Évaluation du niveau initial
L’objectif de cette première étape était de s’assurer que le niveau initial des élèves ne différait pas statistiquement d’un groupe à l’autre. Pour cela, nous avons évalué le niveau des participants en géométrie en questionnant chaque élève sur l’affirmation suivante : je me considère bon élève en géométrie. L’élève devait se situer sur une échelle de Lickert (Matell et Jacoby, 1971) allant de 1 à 7, 7 voulant dire totalement d’accord et 1 voulant dire pas du tout d’accord. Ensuite, tous les élèves avaient 4 minutes pour résoudre un exercice de construction de figure géométrique sur papier, en utilisant les outils classiques (crayon, compas, règle, etc.). La consigne était : Trace un triangle rectangle ABC en B tel que BC = 6 cm et l’angle BAC = 40°. Nous avons observé que le niveau des trois groupes était homogène, tant sur le questionnaire d’auto-évaluation que sur l’exercice de construction. Relativement à ce dernier, nous avons observé un pourcentage de succès très bas pour les trois groupes (respectivement 14,81 %, 3,57 %, et 13,33 %). Il est donc intéressant de noter que des élèves de 5e affichent des difficultés à construire une figure qui peut pourtant paraître simple.

Phase d’entraînement
Au cours de cette phase, qui a duré 6 minutes, tous les élèves de chaque groupe ont effectué des tâches de construction géométrique sur leur support dédié (dessin de segment à main levée, dessin de segment avec utilisation de la règle, construction d’un angle précis en utilisant un rapporteur, utilisation de la gomme pour supprimer les tracés). Cette phase, surtout importante pour les deux groupes utilisant la tablette stylet, nous a permis de nous assurer de leur bonne compréhension de l’utilisation du logiciel. Les élèves du groupe contrôle ont effectué les mêmes tâches sur support papier.

Phase d’apprentissage
Cette phase nous a permis d’évaluer les performances des élèves des trois groupes. L’objectif ici était de travailler sur trois exercices, de même difficulté, portant sur la construction de triangles scalènes :

  • Exercice 1 : Trace le triangle ABC tel que AB = 5,5 cm, BAC = 55°, ABC = 52° ;
  • Exercice 2 : Trace le triangle ABC tel que AB = 6,8 cm, BAC = 31°, ABC = 40° ;
  • Exercice 3 : Trace le triangle ABC tel que AB = 7 cm, BAC = 43°, ABC = 50°.

Chaque élève avait six minutes pour réaliser un exercice.

Phase de transfert
Cette dernière phase avait pour objectif de mesurer la transférabilité de l’apprentissage du support numérique vers le support papier. Pour cela, les élèves de tous les groupes ont effectué deux exercices sur support papier :

  • une tâche de transfert dite « proche » : Trace le triangle ABC tel que AB = 8 cm, BAC = 70°, ABC = 32° ;
  • une tâche de transfert dite « lointaine » : Trace le triangle rectangle ABC en B tel que AB = 4 cm et l’angle BAC = 50°.

La première tâche est dite « proche » parce que l’exercice est similaire à ceux proposés dans la phase d’apprentissage, tandis que la seconde dite « lointaine » implique des connaissances qui n’ont pas été mises en œuvre durant la phase d’apprentissage. Chacune des tâches a duré 4 minutes.

Quels résultats a-t-on obtenus ?

Résultats de la phase d’apprentissage

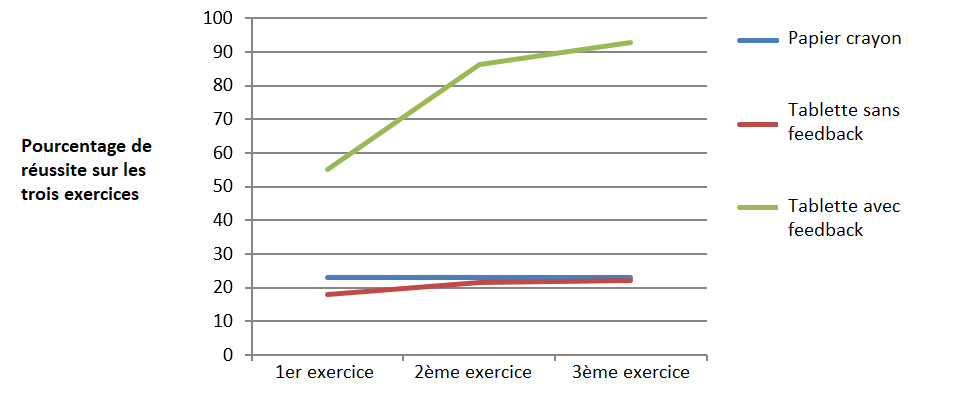
La Figure 3 présente le pourcentage de succès pour les élèves des trois groupes pour chacun des trois exercices de construction de triangle effectués au cours de la phase d’apprentissage. Une comparaison statistique des performances des élèves des différents groupes confirme — ce que la Figure 3 suggère — que les élèves du groupe IntuiGeo avec feedbacks réussissent mieux les exercices que les élèves des groupes papier-crayon et IntuiGeo sans feedbacks. Cependant, l’absence de différence significative entre les performances des élèves des groupes papier-crayon et IntuiGeo sans feedbacks démontre que l’outil en lui-même ne suffit pas mais que c’est la génération de feedbacks correctifs en temps-réel qui permet une amélioration des performances des élèves.

Un autre résultat parait particulièrement intéressant à souligner : le pourcentage de réussite des élèves du groupe IntuiGeo avec feedbacks évolue au cours des exercices pour atteindre 92,86 % pour le troisième exercice. En revanche, nous constatons une stagnation, ou au plus une très légère progression (différence non significative), pour les deux autres groupes, avec un taux de réussite pour le troisième exercice qui avoisine les 20 %. Ces résultats suggèrent non seulement que les élèves du groupe IntuiGeo avec feedbacks comprennent bien les retours fournis par le tuteur mais aussi que, comme précédemment, la génération de feedbacks correctifs en temps-réel qui permet aux élèves de progresser d’un exercice à l’autre.

Pour conclure, l’ensemble des résultats obtenus, à savoir, la similarité entre les groupes papier-crayon et IntuiGeo sans feedbacks, les meilleures performances pour le groupe IntuiGeo avec feedbacks mais aussi l’évolution des performances au cours des exercices observée uniquement pour les élèves bénéficiant de feedbacks correctifs, suggèrent que l’amélioration des performances dans la construction de figures géométriques n’est pas due au support lui-même (papier ou tablette), mais aux fonctionnalités qu’il fournit (ici, les feedbacks correctifs d’IntuiGeo).

Graphique présentant les résultats obtenus. Description détaillée ci-dessous.
Figure 3 – Taux de réussite moyen des élèves obtenu pour chaque exercice effectué au cours de la phase d’apprentissage en fonction du groupe expérimental.

Résultats de la phase de transfert

Le Tableau 1 présente les performances des élèves pour chaque groupe et pour chaque exercice effectué sur support papier au cours de la phase de transfert. Pour la tâche de transfert « proche » (construction d’un triangle scalène), nous remarquons une différence significative en terme de performances entre le groupe IntuiGeo avec feedbacks et les deux autres groupes. En effet, le pourcentage de succès des élèves de ce groupe est de 60 %, contre 26 et 25 % pour les deux autres. Ce résultat très important montre que les compétences acquises sur format numérique à l’aide de la correction du tuteur sont transférées sur le support papier, suggérant une fois de plus l’importance de feedbacks immédiats et personnalisés. Pour la tâche de transfert « lointaine » (construction d’un triangle rectangle), nous ne remarquons pas de différence significative entre les trois groupes. Ce résultat était attendu puisque les compétences requises pour réussir cette tâche n’ont pas été mises en œuvre durant la phase d’apprentissage.

Tableau 1 – Taux de réussite moyen des élèves obtenu pour les tâches de transfert « proche » et « lointaine » effectuées au cours de la phase de transfert.
Tâches Groupe
Contrôle 		Groupe
IntuiGeo sans feedbacks 		Groupe
IntuiGeo avec feedbacks
Triangle scalène25,93 %25 %60 %
Triangle rectangle22,22 %10,71 %23,33 %

Le tableau présente les résultats aux tâches « Triangle scalène » et « Triangle rectangle » pour les trois groupes expérimentaux. Concernant la tâche « Triangle scalène », le groupe contrôle a un taux de réussite de 25,93 %, le groupe IntuiGeo sans Feedbacks, 25 %, et le groupe IntuiGeo avec feedbacks, 60 %. Concernant la tâche « Triangle rectangle », le groupe contrôle a un taux de réussite de 22,22 %, le groupe IntuiGeo sans Feedbacks, 10,71 %, et le groupe IntuiGeo avec feedbacks, 23,33 %.

Que dois-je retenir de cette étude pour ma pratique ?

  • Notre système tutoriel IntuiGeo permet à l’élève de dessiner librement avec le stylet sur tablette tout en manipulant avec ses doigts des outils virtuels réalistes, ce qui a comme conséquence une maîtrise rapide du support numérique en évitant une phase d’entraînement qui peut s’avérer fastidieuse.
  • Nous proposons un mode auteur intuitif qui permet à l’enseignant·e de créer des exercices en dessinant un exemple de solution sur l’interface.
  • Les feedbacks générés « en temps-réel » par le système permettent une amélioration des performances de l’élève et la courbe de progression que nous avons observée au cours des trois exercices nous permet de supposer que les feedbacks générés sont facilement compréhensibles, appropriés et efficaces.
  • Cette étude a aussi démontré la transférabilité de l’apprentissage entre support numérique et support papier, c’est-à-dire que les compétences acquises via l’utilisation d’IntuiGeo sont aussi perceptibles sur un support traditionnel. Cela démontre le bien fondé de notre approche qui simule la condition papier sur tablette (dessin libre avec stylet, manipulation des outils virtuels réalistes avec les doigts), ce qui a pour conséquence de rendre les feedbacks délivrés par le système pertinents quel que soit le support.
  • Il serait intéressant de voir si les effets positifs des feedbacks générés par IntuiGeo perdurent sur le moyen/long terme, en combinant tests d’apprentissage immédiats (c’est-à-dire, comme nous l’avons fait pour cette étude) et différés (c’est-à-dire, à distance de l’utilisation de l’outil).
  • Une piste tout aussi intéressante serait d’évaluer l’impact de l’utilisation d’IntuiGeo avec feedbacks auprès d’élèves de primaire (CM2 par exemple) pour voir si on observe les mêmes effets positifs que ceux obtenus pour les collégiens. Un tel outil pourrait ainsi constituer un support pertinent, efficace et facile à utiliser par les élèves, y compris au cours des premiers pas dans l’apprentissage de la géométrie.

Références

Bhagat, K. K. et Chang, C.-Y. (2015). Incorporating GeoGebra into Geometry Learning-A lesson from India. Eurasia Journal of Mathematics, Science and Technology Education, 11(1), 77-86. https://doi.org/10.12973/eurasia.2015.1307a

Chickering, A. W. et Gamson, Z. F. (1987). Seven Principles for Good Practice in Undergraduate Education. AAHE Bulletin, 39(7), 3-7.

Ghallab, M., Nau, D. et Traverso, P. (2004). Automated planning: theory & practice. Elsevier.

Krichen, O. (2020). Conception d’un système tutoriel intelligent orienté stylet pour l’apprentissage de la géométrie basé sur une interprétation à la volée de la production manuscrite de figures [thèse de doctorat, INSA de Rennes, Rennes, France]. https://tel.archives-ouvertes.fr/tel-03192038

Krichen, O., Anquetil, E. et Girard, N. (2020). IntuiGeo: Interactive tutor for online geometry problems resolution on pen-based tablets. Dans European Conference on Artificial Intelligence (ECAI) 2020 (p. 1842-1849). IOS Press. https://hal.archives-ouvertes.fr/hal-02544384

Krichen, O., Girard, N., Anquetil, E., Corbillé, S. et Renault, M. (2018). Real-time interpretation of handdrawn sketches with extended hierarchical bi-dimensional grammar. Dans 2018 16th International Conference on Frontiers in Handwriting Recognition (ICFHR) (p. 273-278). IEEE. https://hal.inria.fr/hal-01917888

Laborde, C. (2002). Integration of Technology in the Design of Geometry Tasks with Cabri-Geometry. International Journal of Computers for Mathematical Learning, 6(3), 283-317. https://doi.org/10.1023/A\%3A1013309728825

Macé, S. et Anquetil, E. (2009). Eager interpretation of on-line hand-drawn structured documents: The DALI methodology [New Frontiers in Handwriting Recognition]. Pattern Recognition, 42(12), 3202-3214. https://doi.org/10.1016/j.patco

Matell, M. S. et Jacoby, J. (1971). Is There an Optimal Number of Alternatives for Likert Scale Items? Study I: Reliability and Validity. Educational and Psychological Measurement, 31(3), 657-674. https://doi.org/10.1177/001316447103100307

Nkambou, R., Mizoguchi, R. et Bourdeau, J. (2010). Advances in Intelligent Tutoring Systems (vol. 308). Springer Science & Business Media. https://doi.org/10.1007/978-3-642-14363-2

Yan, J., Wang, C., Cheng, W., Gao, M. et Zhou, A. (2018). A retrospective of knowledge graphs. Frontiers of Computer Science, 12(1), 55-74. https://doi.org/10.1007/s11704-016-5228-9

Catégories
Ressources

Wikiradio® (Radio Éducation)

Réaliser et diffuser des productions radiophoniques en équipe, tout en disposant d’outils de feedbacks émotionnels

Logo de la ressource Wikiradio, radio éducation.org

Niveaux

Collège (5e, 4e, 3e) / Lycée

Action/Projet associé(e)

ACTIF

Contact

Nicolas MICHINOV
Laurent HUE

Présentation

Une solution de webradio, adaptée pour l’éducation, la Wikiradio® « Radio Éducation » de l’entreprise Saooti permet aux enseignants et élèves de facilement réaliser et diffuser des productions radiophoniques en équipe, tout en disposant d’outils de feedbacks émotionnels (émoticônes) pour les auditeurs.

L’objectif était d’expérimenter une situation pédagogique dans le cadre du « parcours Avenir » au collège où les élèves sont réunis en équipe pour réaliser et diffuser des épisodes à partir de la webradio avec pour consigne de faire passer un message convainquant sur une formation ou un métier en essayant de capter l’attention des auditeurs et de susciter chez eux des réactions émotionnelles. Les élèves devaient exprimer leur ressenti émotionnel à l’écoute des épisodes réalisés par les pairs en votant sur chacun d’eux à l’aide d’émoticônes qui véhiculent une émotion primaire (joie, tristesse, …) ou une absence d’émotion.

Pour mener à bien ce projet, différentes actions ont été réalisées, l’une dans une démarche de conception centrée utilisateur (CCU) par le laboratoire d’usage des TIC (LOUSTIC), l’autre dans le cadre d’une thèse par un doctorant du LP3C (Anthony Cherbonnier).
Dans les actions de CCU une étude préliminaire sur la compréhension d’un feedback à partir d’émoticônes par des collégiens a été menée, suivi par des entretiens ainsi que des inspections ergonomiques de la webradio et des tests utilisateurs auprès d’enseignants pour optimiser l’utilisation. Une veille documentaire a également été faite auprès du SAIO et de l’ONISEP Bretagne dans le cadre de l’élaboration d’un carnet d’expérimentation diffusé aux collèges partenaires.
Le travail de thèse s’est quant à lui intéressé à la reconnaissance émotionnelle des émoticônes graphiques ainsi qu’à leur usage sur la Wikiradio® « Radio Éducation » dans un contexte scolaire ; au total 18 enseignants de collège ont été impliqués. Bien que les émoticônes soient souvent utilisées dans les environnements numériques pour transmettre des émotions, et qu’une grande diversité d’émoticônes existe, on sait peu de choses sur la façon dont elles transmettent des émotions par rapport à d’autres modes d’expression (Cherbonnier et Michinov, soumis). De la même façon, peu d’études se sont intéressées à leur utilisation dans un contexte scolaire. Dans cette thèse, après avoir conçu et prétesté de « nouvelles » émoticônes qui véhiculent les émotions plus efficacement et plus intensément que les expressions faciales et les émoticônes de Facebook et iOS (Cherbonnier et Michinov, 2021), celles-ci ont été implémentées sur la Wikiradio® afin d’étudier comment elles sont utilisées en contexte scolaire pour exprimer les émotions à l’égard des émissions réalisées par des pairs. Parmi d’autres résultats, les évaluations ont montré un très bon usage des émoticônes (70 %) pour exprimer le ressenti émotionnel à l’écoute des émissions.

Capture d'écran du tableau de bord administrateur. Description détaillée ci-dessous.
(a) Tableau de bord (administrateur)
Capture d'écran illustrant le studio administrateur. Description détaillée ci-dessous.
(b) Studio (administrateur)
Capture d'écran présentant les podcasts accessibles aux auditeurs. Description détaillée ci-dessous.
(c) Podcast du collège (auditeur)
Capture d'écran illustrant les réactions des auditeurs sur un épisode. Description détaillée ci-dessous.
(d) Réactions auditeurs (auditeur)

Disponibilité

La Wikiradio® est accessible au grand public en tant qu’auditeur, à partir de la page internet qui lui est dédiée. L’utilisation de la Wikiradio® pour réaliser des productions radiophoniques est aujourd’hui possible pour tous les établissements scolaires qui le souhaitent. Il est nécessaire pour cela de faire la demande auprès de la société Saooti qui accompagnera les équipes pédagogiques (installation d’un studio de radio, ouverture d’un canal pour l’établissement, formations aux outils et méthodes, etc.).

En savoir plus
Catégories
Ressources

Logiciel pédagogique Kassis Collège

Créer des séquences pédagogiques facilitant les interactions avec les élèves

Logo du logiciel KASSIS

Niveaux

Collège (5e, 4e, 3e) / Lycée

Action/Projet associé(e)

ACTIF

Contact

Éric ANQUETIL

Présentation

À partir d’une solution pour l’enseignement supérieur d’aide à l’apprentissage en présentiel sur tablette-stylet conçue par l’INSA Rennes, la société Learn&Go a développé le logiciel Kassis Collège. Il permet à l’enseignant de créer des séquences pédagogiques facilitant les interactions avec les élèves en délivrant des feedbacks collectifs en classe, notamment par le biais de quiz graphiques innovants. La solution est en cours d’adaptation pour être accessible depuis n’importe quel navigateur web et donc tous types de supports (tablette, PC, smartphone) et environnements (Windows, iOS, Android…). Un réseau local a été conçu pour faciliter le fonctionnement en classe. L’équipe de recherche IntuiDoc de l’IRISA a enrichi la solution par l’organisation automatisée des réponses graphiques des élèves en 2D et 3D (clustering intelligent, carte de saillance) afin d’en faciliter l’analyse et donc les feedbacks immédiats que l’enseignant pourra donner aux élèves.

Pour les phases de conception de Kassis Collège, de nombreuses actions ont été déployées par le LOUSTIC telles que des entretiens avec les enseignants, des sessions de démonstration, des inspections ergonomiques durant la conception, des tests utilisateurs auprès d’élèves et d’enseignants et un questionnaire sur les besoins des enseignants.

Pour étudier les effets sur l’apprentissage en sciences d’activités individuelles ou collaboratives de génération de schémas sur tablette avec stylet, trois expérimentations ont été réalisées en classe de 5e avec la fonctionnalité de dessin de Kassis Collège, dans le cadre d’une thèse au LP3C. De manière générale, les résultats obtenus ont montré que la génération de schémas reste une activité appréciée mais complexe pour des collégiens, y compris lorsqu’elle est guidée, et qu’elle n’entraîne pas de bénéfices par rapport à un texte illustré (Rochat et al., 2020). Le travail de génération en groupe, rendu possible par le développement d’une application spécifique dans le projet, n’a pas permis d’améliorer la qualité des schémas générés ou encore l’apprentissage. Toutefois, nos résultats démontrent que la qualité des interactions dans les dyades influence la qualité des apprentissages.

D’autre part, deux études quasi-expérimentales ont été réalisées, dans le cadre d’un post-doctorat au LP3C, auprès de collégiens en classe de 4e et 3e. L’objectif était d’étudier les effets de l’utilisation de la tablette et de certaines fonctionnalités du logiciel Kassis Collège en mettant en place des méthodes pédagogiques innovantes qui reposent sur l’apprentissage par les pairs. Dans l’une de ces études, les élèves devaient dessiner individuellement un schéma fonctionnel du système respiratoire humain sur une tablette à l’aide d’un stylet, avant et après avoir discuté avec leurs pairs dans des groupes de deux, trois ou quatre élèves (ou après avoir réfléchi seul dans la condition contrôle). Pour alimenter les discussions, les élèves de la classe recevaient un feedback collectif qui se présentait sous la forme d’une série de vignettes correspondant au schéma de chaque élève. Les résultats ont révélé que le gain d’apprentissage était plus important pour les élèves qui avaient discuté en groupes de quatre que pour ceux des autres conditions, et ceci plus chez les filles que chez les garçons (Corrégé et Michinov, soumis).

Capture d'écran de la page d'accueil (compte enseignant). Description détaillée ci-dessous.
(a) Page d’accueil du compte enseignant
Capture d'écran de la page d'accueil "Création d'exercices" (compte enseignant). Description détaillée ci-dessous.
(b) Page de création d’exercices
Capture d'écran de productions d'élèves au quiz "Miniatures". Description détaillée ci-dessous.
(c) Production élèves quiz « Miniatures »
Capture d'écran de productions d'élèves au quiz "Carte chaleur". Description détaillée ci-dessous.
(d) Production élèves quiz « Carte chaleur »

Disponibilité

L’INSA-IRISA va poursuivre les développements et réflexions autour du produit Kassis Collège afin de pouvoir l’adapter également à d’autres contextes d’enseignements, notamment pour l’enseignement hybride (distance-présence).

En savoir plus
Catégories
Ressources

Logiciel éducatif IntuiGeo

Un système tutoriel intelligent pour l’apprentissage de la géométrie au collège

Logo du logiciel IntuiGeo

Niveaux

Collège (5e, 4e, 3e)

 

Action/Projet associé(e)

ACTIF — TRIANGLE

 

Contact

Éric ANQUETIL
Éric JAMET

Présentation

Le travail de recherche au sein de l’équipe IntuiDoc (IRISA) a consisté à concevoir un logiciel sur tablette orienté stylet intitulé IntuiGeo (système tutoriel intelligent), pour l’apprentissage de la géométrie au collège. L’objectif est de permettre à l’élève de dessiner librement avec le stylet des figures géométriques tout en manipulant des outils virtuels réalistes. Pour cela, le premier axe de recherche a consisté à concevoir un moteur d’Intelligence Artificielle (IA) pour la reconnaissance de tracés manuscrits, avec une connaissance du domaine modélisée par de grammaires visuelles bi-dimensionnelles (Krichen et al., 2018). L’objectif est ensuite d’élaborer des feedbacks personnalisés en temps-réel à l’élève. Pour ce faire, le deuxième axe de recherche a consisté à définir un moteur tutoriel intelligent, permettant de créer des exercices et de superviser les réalisations des élèves. Un mode auteur intuitif a été développé, permettant à l’enseignant de créer des exercices en construisant un exemple de solution sur le logiciel. L’originalité de l’approche, publiée à ECAI (Krichen et al., 2020), est de se baser sur une modélisation hybride de la connaissance du domaine. La connaissance déclarative (relative au savoir) est modélisée par des graphes de connaissance et permet de fournir des feedbacks de correction (exemple : la longueur de ton segment est incorrecte). La connaissance procédurale (relative au savoir-faire) est modélisée par des règles de planification. C’est ce qui permet au système tutoriel de synthétiser des stratégies de résolution de problème et de générer, à partir de ces stratégies, des feedbacks de guidage (exemple : utilise le compas de telle façon pour construire un triangle équilatéral).

Pour la phase de conception du logiciel, de nombreuses actions ont été déployées par le LOUSTIC telles qu’un benchmark, des entretiens avec les enseignants, un questionnaire en ligne sur les besoins, des inspections ergonomiques, des tests utilisateurs auprès d’enseignants et d’élèves et la constitution d’un comité d’expert en géométrie. Des expérimentations en classe ont été réalisées par le LP3C pour apprécier les effets des feedbacks correctifs en temps réel (Colliot et al., en révision). Des élèves ont été partagés en trois groupes (élèves utilisant la tablette avec feedback, élèves travaillant sur papier, élèves utilisant la tablette sans feedback). Les résultats ont montré que les élèves du premier groupe obtiennent des résultats significativement meilleurs, que ce soit sur leurs supports respectifs, ou sur une tâche de transfert sur papier, que ceux du deuxième et troisième groupe. Ces résultats montrent que le retour d’information en temps réel généré par l’IA peut améliorer les performances d’apprentissage des enfants, ici en géométrie. Cet outil est développé et évalué en collaboration avec l’équipe IntuiDoc (IRISA), le laboratoire LP3C et le LOUSTIC, avec les collèges partenaires de l’académie de Rennes.

Capture d'écran illustrant le mode création d'exercice pour l'enseignant. Description détaillée ci-dessous.
(a) Exemple de création d’exercice (enseignant)
Capture d'écran illustrant le mode création d'exercice pour l'enseignant. Description détaillée ci-dessous.
(b) Exemple de création d’exercice (enseignant)
Capture d'écran illustrant le mode résolution d'exercice par l'élève. Description détaillée ci-dessous.
(c) Exemple de résolution d’exercice (élève)
Capture d'écran illustrant le mode résolution d'exercice par l'élève lorsqu'il demande de l'aide. Description détaillée ci-dessous.
(d) Exemple de résolution avec « Demande d’aide » (élève)

Disponibilité

IntuiGeo est disponible au grand public pour une utilisation sur tablette stylet Windows.

En savoir plus
Catégories
e-FRAN Toutes les actions et projets

Projet ACTIF

Logo du projet ACTIF

Outils numériques et méthodes pédagogiques pour l’apprentissage « actif » et « collaboratif »

Le projet ACTIF visait à expérimenter chez les collégiens des outils numériques et des méthodes pédagogiques facilitant l’apprentissage « actif » et « collaboratif » à partir de tablettes en donnant un rôle déterminant aux feedbacks donnés à chaque élève, à l’ensemble de la classe ou à des équipes d’élèves. Une démarche de conception centrée utilisateur a été utilisée dans l’ensemble du projet afin d’optimiser l’adéquation des dispositifs aux besoins des utilisateurs. Sur cette base, trois outils ont été conçus et/ou optimisés, puis évalués par les partenaires auprès de 1 798 élèves. Le premier (IntuiGeo) est un outil d’apprentissage de la géométrie sur tablette basé sur l’interprétation automatique des formes dessinées et un tuteur intelligent permettant de fournir aux élèves des feedbacks automatiques. Le second (Kassis Collège) est un outil sur tablette dont l’objectif est de favoriser les interactions dans la classe en permettant d’y réaliser des activités variées (par exemple, dessins au stylet, quiz graphiques) seul ou en groupe. Il permet également à l’enseignant de fournir aux élèves des feedbacks collectifs à partir de leurs productions. Enfin, une Wikiradio® a été optimisée dans le cadre du projet pour permettre aux élèves de fournir des feedbacks émotionnels dans un travail d’équipe.

En savoir plus
Accéder au rapport de l’HCÉRES
© Vidéo YouTube : projet ACTIF

Responsable projet :
Laurent BLANES
Responsables scientifiques :
Éric JAMET
Nicolas MICHINOV
Éric ANQUETIL
Coordinateur projet :
Maxime ROBERT

Quelques chiffres

Académie de Rennes

1 144 K€ de subventions

14 collèges
1 798 élèves

Carte de France indiquant les départements impliqués dans le projet. Description détaillée ci-dessous.

Résultats obtenus

Un système de tutorat intelligent pour l’apprentissage de la géométrie sur tablette a été conçu par l’équipe informatique du projet. Il permet d’interpréter en temps réel les formes réalisées par les élèves et leur fournir des guidages et feedbacks personnalisés. Ses effets bénéfiques sur les apprentissages ont été démontrés.
Concernant l’outil Kassis Collège, les études réalisées ont notamment montré 1) que l’activité d’apprentissage par le dessin a été très appréciée par les élèves, mais aussi qu’elle reste complexe à réaliser, que ce soit seul ou en collaboration et 2) que les feedbacks collectifs produisent des effets positifs sur l’apprentissage en stimulant les discussions entre pairs, particulièrement dans les groupes de 4 élèves.
Une Wikiradio® a été optimisée notamment par l’ajout d’une fonctionnalité de feedback émotionnel. L’évaluation a montré un très bon usage de celle-ci (70 % d’utilisation).

Préconisations

Les différentes études ont montré que des outils numériques incluant des feedbacks de formes variées ont permis de favoriser leurs apprentissages et/ou les interactions entre pairs. À titre d’exemple, ce n’est pas le simple passage du papier aux tablettes qui augmentent les performances dans les études sur la géométrie mais bien le fait de fournir des feedbacks dans l’application. Nos études montrent également globalement un niveau d’intérêt élevé pour les activités individuelles et collaboratives sur tablettes. Toutefois, le fait de passer en mode collaboratif ne garantit pas systématiquement une augmentation des performances. De nombreux facteurs influencent l’efficacité du travail de groupe, par exemple la taille des groupes dans notre étude sur les feedbacks collectifs ou la qualité des interactions entre élèves dans la tâche de dessin collaboratif.

Prolongements du projet

Certains des partenaires du projet sont engagés dans la construction d’un projet ANR sur le dessin sur tablette. De nouvelles collaborations sont prévues également avec l’académie de Rennes.

En savoir plus sur la suite et le déploiement du projet ACTIF
Catégories
Thèses

Quand lire vite ne suffit pas : le rôle de l’expressivité

Erika GODDE

Niveaux

Du CP au début du collège

 

 

Public

Enseignant·e·s d’élémentaire, professeur·e·s de français en collège

 

Contact

Erika GODDE — Voir ses publications

Laboratoires LPNC et GIPSA-Lab

Action/Projet associé(e)

FLUENCE

Ressource(s) associée(s)

Échelle MultiDimensionnelle de Fluence — ELARGIR

© Vidéo YouTube : Soutenance Thèse GODDE RASSAT Erika
Ce résumé
Manuscrit de thèse

À quelles questions cette étude tente-t-elle de répondre ?

Ce travail de recherche s’intéresse à la prosodie pendant la lecture à voix haute, que l’on désigne parfois comme la capacité de l’élève à lire en « mettant le ton ». Les deux composantes essentielles à la prosodie sont le phrasé (rythme et placement des pauses) et l’expressivité (modulation de la voix, accentuations…). Trois questions principales sont posées ici : (1) comment peut-on évaluer la prosodie d’un apprenti lecteur, (2) comment la prosodie se développe-t-elle pendant l’apprentissage, (3) quel est son rôle, notamment pour la compréhension du texte lu. Un outil pratique et accessible aux enseignants a été développé, permettant d’évaluer la prosodie en lecture des élèves et pas seulement leur vitesse de lecture. Cet outil a été validé par comparaison à des mesures acoustiques (par exemple, des mesures objectives de la durée et du placement des pauses). Ces différents outils nous ont permis de décrire le développement de la prosodie en lecture et d’étudier sa relation avec la compréhension des textes lus.

Pourquoi ces questions sont-elles pertinentes ?

Question 1 : comment évaluer la prosodie.

L’évaluation des compétences en lecture se fait souvent, dans les écoles de France et dans la recherche, par mesure de la vitesse, c’est-à-dire en comptant le nombre de mots correctement lus par minute. Cette mesure de vitesse, abusivement appelée fluence, permet une évaluation quantitative, rapide et facile à réaliser en classe. Cependant, la consigne donnée aux enfants étant une consigne de vitesse, ils lisent le plus vite possible sans forcément accorder de l’attention au sens du texte lu. Des études suggèrent que cette méthode serait insuffisante pour évaluer l’ensemble des compétences en lecture (Dowd et Bartlett, 2019 ; O’Connor, 2018) et qu’il serait préférable de privilégier une évaluation de la lecture qui prendrait en compte non seulement la vitesse et la précision de décodage, mais également la prosodie du lecteur. Comme plusieurs auteurs anglophones (Dowhower, 1991 ; Kuhn et al., 2010 ; Rasinski, 2004), nous pensons qu’il est pertinent de définir la fluence en lecture comme une compétence globale incluant la précision du décodage, la vitesse de lecture, mais aussi la prosodie, notamment le phrasé et l’expressivité. Or, il n’existe actuellement pas d’outil pour évaluer la prosodie en classe.

Question 2 : comment la prosodie en lecture se développe-t-elle.

Des études dans diverses langues montrent que toutes les dimensions de la fluence, telle que nous venons de la définir, se développent simultanément dès le début de l’apprentissage de la lecture, mais pas forcément au même rythme (pour une synthèse, voir Godde et al., 2020). Au début de l’apprentissage, le décodage se met en place et la vitesse de lecture s’accélère, avec aussi une amélioration rapide du phrasé. Dès le CP, les compétences en phrasé sont révélatrices des futures acquisitions en lecture (Lai et al., 2014). L’expressivité est plus longue à apparaître et continue à se développer au-delà de l’école primaire, particulièrement quand les textes proposés aux élèves se complexifient (Alvarez-Canizo et al., 2020 ; Kuhn et Schwanenflugel, 2019). Il est probable que ce développement dépende des caractéristiques de la langue, et aucune étude développementale de la prosodie en lecture n’a été faite en langue française. Décrire finement ce développement permettra d’ouvrir des pistes pour les actions pédagogiques ciblées en fonction des étapes développementales.

Question 3 : rôle de la prosodie pour la compréhension.

Plusieurs études en anglais et en espagnol ont mis en évidence une relation entre les dimensions prosodiques de la fluence et la compréhension de textes écrits (pour une synthèse, voir Godde et al., 2020). De plus, certaines études suggèrent que le sens de cette relation évolue au cours du temps. Dans les premières années d’apprentissage, c’est la compréhension du texte qui entrainerait une meilleure prosodie en lecture à voix haute. Plus tard, chez le bon lecteur, il est possible que la prosodie soit utilisée pour faciliter la compréhension de textes lus. Ainsi, chez les adultes comme chez les enfants, on a observé que la confrontation a un texte complexe ou à des phrases ambiguës entraine une accentuation de la prosodie, avec des pauses plus longues et une intonation plus marquée. Mieux comprendre cette relation entre prosodie et compréhension en lecture devrait apporter des informations utiles pour l’enseignement de la compréhension.

Pour conclure, les résultats des recherches menées autour de la prosodie en lecture et de sa relation avec les compétences en compréhension de textes écrits, suggèrent que la prosodie joue un rôle important dans le développement des compétences en lecture. Étudier l’acquisition de la prosodie en lecture chez l’élève français est une première étape indispensable pour que cette dimension soit mieux comprise, mieux prise en compte et enseignée. C’est l’objectif de nos études, qui visent à approfondir les connaissances actuelles sur le développement de la prosodie au cours de l’apprentissage. Ces recherches ont permis le développement d’un outil qui permettra aux enseignants d’évaluer les compétences en lecture des élèves en prenant en compte la prosodie.

Quelle méthodologie de recherche a-t-on utilisée ?

Nous avons enregistré 323 enfants du CE1 à la 5e et 20 adultes en train de lire à voix haute les deux mêmes textes : un texte narratif et un dialogue. Les enfants de CE1 ont été suivis pendant trois ans. Ils ont été de nouveau enregistrés en CE2 puis en CM1 sur la lecture des mêmes textes. Pour chaque participant et à chaque lecture, nous avons enregistré leur voix et leur respiration.

Pour mesurer la prosodie des lectures enregistrées (Question 1), nous avons utilisé trois outils différents. Le premier outil est une grille d’évaluation subjective inspirée de celle existant pour l’anglais (Rasinski, 2004) et adaptée pour le français (Godde et al., sous presse). Cette grille nommée « Echelle Multi-Dimensionnelle de Fluence » (EMDF) comprend quatre dimensions à évaluer : vitesse, décodage, phrasé et expressivité. À chaque dimension est attribuée un score de 1 à 4, pour un score maximum de 16. Les lectures ont été évaluées par des chercheurs experts, des enseignants et des étudiants. Le second outil est l’évaluation acoustique objective : grâce à un logiciel spécialisé, nous mesurons, pour chaque enregistrement, différents paramètres comme la durée des pauses, la position de la respiration pendant les pauses, la variation de hauteur de la voix et la position de cette variation dans la phrase etc. Finalement, un troisième outil a été développé au laboratoire Gipsa-lab à partir des deux précédents (Godde et al., 2019). Il s’agit d’une formule mathématique qui permet, à partir des données acoustiques prises sur une lecture, de prédire automatiquement quels scores à l’EMDF devraient être attribués à cette lecture.

Le développement de la prosodie a pu être décrit (Question 2) grâce aux résultats obtenus par les enfants des différents niveaux scolaires, à l’EMDF et aux analyses acoustiques. Des analyses statistiques nous ont permis de vérifier entre quels niveaux scolaires les scores augmentent significativement ou, au contraire, stagnent. Nous nous sommes notamment attachés à décrire l’acquisition de la coordination entre la lecture et la respiration, en portant une attention particulière, pendant les pauses respiratoires, au délai entre l’inspiration et le début de l’articulation.

Afin d’étudier le lien entre fluence et compréhension de textes écrits (Question 3), les enfants testés ont également réalisé deux tests de compréhension :

  • un test de compréhension globale de texte, où les enfants doivent lire un texte long et répondre ensuite aux questions posées.
  • un test de compréhension plus locale (au niveau de la phrase ou du paragraphe) nommé « texte labyrinthe ». Les enfants doivent lire un texte dans lequel, pour un mot sur sept, quatre propositions sont données. L’enfant doit entourer le bon mot avant de poursuivre sa lecture.

Afin de contrôler leur influence, nous avons aussi évalué certaines compétences générales connues pour avoir une influence sur la compréhension : le raisonnement non-verbal, la compréhension orale, le niveau de vocabulaire et la vitesse de lecture.

Quels résultats a-t-on obtenus ?

Les premiers résultats concernent l’évaluation de la prosodie — et plus généralement de la fluence — chez l’apprenti lecteur (notre 1ère question de recherche). Nous avons vérifié que la grille d’évaluation subjective EMDF utilisable à l’école, est un outil sensible (c’est-à-dire qui permet bien de différencier les élèves faibles, moyens ou forts), fiable (c’est-à-dire, par exemple, qui ne donne pas des résultats différents en fonction des personnes qui l’utilisent) et valide (c’est-à-dire qui mesure bien ce que l’on souhaite mesurer) pour mesurer la fluence incluant la prosodie du CE1 au CM2. Cette grille d’évaluation permet d’obtenir davantage d’informations que la seule mesure du nombre de mots par minute. Par exemple, l’analyse des scores de chacune des dimensions permet de différencier les stratégies mises en place par les apprentis lecteurs. Pour utiliser cette grille, nous avons constaté qu’il est important de suivre un protocole strict et d’utiliser plusieurs textes pour avoir un score représentatif des compétences de l’enfant. Cet outil pourra facilement être utilisé en classe pour compléter l’évaluation de la vitesse en lecture.

L’analyse acoustique des lectures est, pour des raisons techniques, essentiellement utilisable en recherche afin d’obtenir une analyse fine des productions orales et d’accéder aux mécanismes cognitifs sous-jacents. Ici elle nous a permis d’observer l’acquisition de la planification des pauses et de la respiration. C’est un outil très précis mais qui ne renseigne pas directement sur les compétences en lecture. Finalement l’analyse automatique développée au GIPSA-lab est aussi un outil dédié à la recherche. Il a été utilisé pour les évaluations répétées des mêmes enfants du CE1 au CM1. C’est un outil intéressant pour les évaluations multiples, car beaucoup plus consistant et précis que la grille utilisée par des juges humains. Il permet de capter des variations fines, et est donc particulièrement utile pour évaluer à plusieurs reprises les progrès d’enfants.

Relativement à notre deuxième question de recherche, les analyses réalisées à l’aide de ces outils nous ont permis d’identifier les grandes étapes de développement des quatre dimensions de la fluence. Les compétences de décodage, vitesse et phrasé se développent rapidement du CE1 au CM1 puis plus lentement, avec en 5e des compétences assez proches de celles des adultes. Il semble y avoir une étape clé entre CE2 et CM1 : la planification des pauses et la coordination avec la respiration sont alors acquises, il n’existe quasiment plus de pauses mal placées. Nous avons également observé que les lecteurs de CE1-CE2 s’appuient beaucoup sur la ponctuation pour placer correctement leurs pauses, particulièrement respiratoires. L’expressivité se développe à un autre rythme. Les scores d’expressivité sont très faibles en début d’apprentissage et augmentent lentement. Ils atteignent en 5e un score maximum qui reste inférieur aux scores des lecteurs experts. Cette compétence semble donc plus longue et complexe à acquérir. Nous avons aussi observé que le phrasé et l’expressivité de l’élève de CM1 ne dépendent ni de ses capacités antérieures de décodage ni de sa vitesse de lecture. Par contre, le phrasé semble aider l’élève à décoder, probablement parce qu’il renforce l’analyse de la syntaxe du texte.

Finalement, ces données nous ont également permis de préciser la nature du lien entre la prosodie et la compréhension (notre 3ème question de recherche). Comme dans d’autres langues, nous montrons que la prosodie des apprentis lecteurs français semble bien liée à leur capacité à comprendre les textes lus alors que leur vitesse de lecture n’est pas corrélée à leur score de compréhension. Une étude longitudinale du CE1 au CM1 a permis de préciser la nature de ce lien entre prosodie et compréhension, c’est-à-dire de savoir si l’on est capable de lire avec une bonne prosodie parce qu’on comprend les textes qu’on lit, ou si on comprend les textes qu’on lit parce qu’on a développé de bonnes capacités de lecture avec prosodie. Nos données penchent en faveur de la seconde hypothèse. Pour être plus précis, le niveau d’expressivité en CE1 prédit la compréhension en CE2 et le phrasé en CE2 prédit la compréhension en CM1, indépendamment des autres facteurs mesurés (c’est-à-dire, la vitesse, le décodage, le niveau de vocabulaire et de compréhension orale). La prosodie semble donc aider au développement des compétences en compréhension de textes lus.

Que dois-je retenir de cette étude pour ma pratique ?

  • Une évaluation fine des compétences en lecture devrait tenir compte non seulement de la précision du décodage et de la vitesse de lecture, mais aussi du phrasé (par exemple la capacité à respecter la syntaxe par un usage approprié de pauses pendant la lecture) et de l’expressivité (par exemple la capacité à moduler sa voix en fonction du type de phrase, à accentuer certains mots pour les mettre en valeur) au cours de lectures à haute voix.
  • La grille d’évaluation EMDF que nous proposons (Godde et al., sous presse) est utilisable par les enseignants dans le cadre d’une évaluation des compétences en lecture. Cette grille peut également servir aux élèves comme outil d’auto-évaluation leur permettant de visualiser ce qui est attendu d’eux en lecture à haute voix.
  • Au-delà de l’évaluation, faire lire l’élève à haute voix en portant attention aux marqueurs prosodiques — phrasé et expressivité — permet dès le début de l’apprentissage de porter l’attention sur la compréhension. Ce travail est particulièrement important du CE1 au CM1, période durant laquelle ces compétences se développent rapidement, mais n’en demeure pas moins utile au-delà de l’école élémentaire, lorsque les textes deviennent de plus en plus complexes.
  • L’enseignement explicite du phrasé et de l’expressivité, comme celui du rythme et des nuances en musique, pourrait aider les élèves à progresser en lecture et en compréhension écrite. Cet enseignement pourrait comporter des temps de modélisations, où l’enseignant fait entendre aux élèves une lecture expressive, des temps d’analyse pour expliciter ce qui rend une lecture expressive, et des temps d’entrainement.
  • Un entrainement régulier à la lecture à haute voix peut paraitre difficile et fastidieux à mettre en œuvre dans les classes. Des outils numériques proposant des exercices de lecture en autonomie pourraient faciliter cette mise en œuvre, comme le karaoké de lecture ELARGIR, actuellement développé dans le cadre du projet e-FRAN Fluence. L’utilisation d’un tel outil permet un travail individuel et en autonomie d’un ou de plusieurs élèves simultanément.

Références

Alvarez-Canizo, M., Cueva, E., Cuetos, F. et Suarez-Coalla, P. (2020). Reading fluency and reading comprehension in Spanish secondary students. Psicothema, 32(1), 75-83. https://doi.org/10.7334/psicothema2019.196

Dowd, A. J. et Bartlett, L. (2019). The Need for Speed: Interrogating the Dominance of Oral Reading Fluency in International Reading Efforts. Comparative Education Review, 63(2), 189-212. https://doi.org/10.1086/702612

Dowhower, S. L. (1991). Speaking of prosody: Fluency’s unattended bedfellow. Theory into Practice, 30(3), 165-175. https://doi.org/10.1080/00405849109543497

Godde, E., Bailly, G. et Bosse, M.-L. (2019). Reading Prosody Development: Automatic Assessment for a Longitudinal Study. Dans Speech and Langage Technology for Education 2019 (SLaTE). https://doi.org/10.21437/SLaTE.2019-20

Godde, E., Bosse, M.-L. et Bailly, G. (2020). A review of reading prosody acquisition and development. Reading and Writing, 33(2), 399-426. https://doi.org/10.1007/s11145-019-09968-1

Godde, E., Bosse, M.-L. et Bailly, G. (sous presse). Échelle Multi-Dimensionnelle de Fluence : nouvel outil d’évaluation de la fluence en lecture prenant en compte la prosodie, étalonné du CE1 à la 5ème. L’Année psychologique.

Kuhn, M. R. et Schwanenflugel, P. J. (2019). Prosody, pacing, and situational fluency (or why fluency matters for older readers). Journal of Adolescent & Adult Literacy, 62(4), 363-368. https://doi.org/10.1002/jaal.867

Kuhn, M. R., Schwanenflugel, P. J. et Meisinger, E. B. (2010). Aligning theory and assessment of reading fluency: Automaticity, prosody, and definitions of fluency. Reading Research Quarterly, 45(2), 230-251. https://doi.org/10.1598/RRQ.45.2.4

Lai, S. A., George Benjamin, R., Schwanenflugel, P. J. et Kuhn, M. R. (2014). The Longitudinal Relationship Between Reading Fluency and Reading Comprehension Skills in Second-Grade Children. Reading & Writing Quarterly, 30, 116-138. https://doi.org/10.1080/10573569.2013.789785

O’Connor, R. E. (2018). Reading fluency and students with reading disabilities: How fast is fast enough to promote reading comprehension? Journal of Learning Disabilities, 51(2), 124-136. https://doi.org/10.1177/0022219417691835

Rasinski, T. V. (2004). Assessing reading fluency. Pacific Resources for Education and Learning (PREL).

Catégories
Ressources

Logiciel d’évaluation EELENE

Echelle d’Evaluation en Littératie Emergente et Numératie Emergente

Logo du projet LINUMEN, littératie et numératie émergentes par le numérique

Niveaux

Moyenne et Grande sections de maternelle

Action/Projet associé(e)

LINUMEN

Contact

Youssef TAZOUTI

Présentation

L’application EELENE (Echelle d’Evaluation en Littératie Emergente et Numératie Emergente) permet de tester les compétences des enfants de l’école maternelle en littératie émergente (LE) et en numératie émergente (NE). Il s’agit d’une échelle d’évaluation dont le but est de permettre aux chercheurs et/ou aux enseignants de situer le niveau précis de l’enfant au regard des différentes compétences indispensables à travailler. Cette version comprenait 14 épreuves en littératie émergente (c’est-à-dire, connaissance des lettres, conscience phonologique et langage oral) et 11 épreuves en numératie émergente  (c’est-à-dire, connaissance des chiffres, dénombrement, cardinalité, sériation, …). Une seconde version de l’application sera développée courant de l’année 2021-2022.

Capture d'écran de la page d'accueil (page de connexion) de l'application

Disponibilité

L’application EELENE a été conçue pour être utilisée par des enseignants et des élèves de moyenne et grande section de maternelle. Actuellement, elle n’est pas disponible pour de libres utilisations en classe, son usage étant exclusivement réservé à la recherche. À terme, elle sera proposée en téléchargement via ce site et les stores Androïd et iOS.

En savoir plus
Catégories
e-FRAN Toutes les actions et projets

Projet LINUMEN

Logo du projet LINUMEN, littératie et numératie émergentes par le numérique

LIttératie et NUMératie Emergentes par le Numérique

Le projet LINUMEN avait comme objectifs de concevoir et de tester un dispositif numérique proposant des activités pour développer les compétences en littératie et numératie émergentes (LNE) d’enfants d’âge préscolaire afin de préparer au mieux leur entrée dans les apprentissages de la lecture, de l’écriture ainsi que ceux relevant des compétences mathématiques au CP. Le projet se proposait également de tester l’acceptabilité du dispositif par les enseignants. Après une phase de co-conception de deux ans (mars 2017 – août 2018), des enseignants-chercheurs et des acteurs éducatifs ont élaboré deux applications éducatives sur tablette tactile. La première application (EELENE) permet de tester les compétences des enfants de l’école maternelle en LNE. La seconde application (AppLINOU : Apprendre avec Linou en maternelle) permet aux enfants de développer les compétences en LNE dans le contexte de la classe. AppLINOU comporte une vingtaine d’activités présentant certaines qualités éducatives (feedback, l’étayage, etc.) et recouvrant cinq périodes du début de la MS jusqu’à la fin de la GS. Entre octobre 2018 et mars 2021, l’efficacité du dispositif a été testée selon une méthodologie expérimentale et longitudinale. 750 élèves scolarisés dans 32 écoles et 72 classes ont été suivis du début de MS jusqu’à la mi-CP.

En savoir plus
Accéder au rapport de l’HCÉRES
© Vidéo YouTube : Projet LINUMEN

Responsable projet :
Youssef TAZOUTI
Cheffe de projet :
Héléna PETIAU

Quelques chiffres

Académie de Nacy-Metz

800 K€ de subventions

32 écoles maternelles
774 élèves

Carte de France indiquant le département impliqué dans le projet. Description détaillée ci-dessous.

Résultats obtenus

Dans le cadre du suivi de la cohorte LINUMEN, nous avons récupéré les évaluations du début de CP afin de comparer les élèves du groupe expérimental et ceux du groupe contrôle avec l’échantillon national. Les résultats montrent qu’une plus faible proportion d’élèves du groupe expérimental est considérée comme ayant des difficultés importantes en français et en mathématique en comparaison des élèves du groupe contrôle et de l’échantillon national. De même, un pourcentage plus important d’élèves du groupe expérimental a une bonne maitrise des compétences évaluées en français et en mathématiques en comparaison avec ceux du groupe contrôle et de l’échantillon national. Par ailleurs, des analyses de régression multiniveaux de croissance ont montré un impact positif de l’intervention sur la progression des élèves en début CP. Toute chose égale par ailleurs, les élèves du groupe expérimental progressent significativement plus que les élèves du groupe contrôle aussi bien en français qu’en mathématique. 

Préconisations

Le projet LINUMEN a permis de questionner les conditions dans lesquelles certaines applications éducatives présentées sur tablette peuvent être efficaces dans le cadre scolaire.  Notre objectif est de rendre accessible les résultats de la recherche aux acteurs éducatifs (Inspecteurs de l’Éducation nationale, conseillers pédagogiques et enseignants) par la rédaction d’une note de synthèse.

Prolongements du projet

Les deux applications développées dans le cadre du projet LINUMEN : AppLINOU (Apprendre avec Linou en maternelle) et EELENE (Echelle d’Evaluation en Littératie Emergente et en Numératie Emergente) bénéficient du soutien financier de SAYENS (SATT) pour un projet de maturation durant l’année 2021-2022. Le montant de l’investissement est de 100 500 euros.  L’objectif de la maturation est de renforcer la portabilité du code et de compléter les fonctionnalités des applications avec des activités supplémentaires. Cela permettra de disposer d’un dispositif déployable sur toutes les tablettes (Android et iOs) et adaptable aux différents besoins des élèves et des enseignants en termes de modalités et de rythme d’apprentissage. Ce processus se fera dans le cadre d’une co-maturation avec la société LearnEnjoy qui bénéficie déjà d’une forte notoriété dans le domaine de l’EdTech et qui apportera son expertise sous forme d’accompagnement technique dans le domaine du développement des applications éducatives.

Catégories
Ressources

Logiciel éducatif AppLINOU

Apprendre avec Linou en maternelle

Illustration de LINOU, mascotte de l'application AppLinou

Niveaux

Moyenne et Grande sections de maternelle

Action/Projet associé(e)

LINUMEN

Contact

Youssef TAZOUTI

Logo de l'application AppLinou

Présentation

Issue d’un processus de co-conception entre des chercheurs de l’Université de Lorraine et des acteurs éducatifs de l’académie Nancy-Metz et la start-up LearnEnjoy, l’application AppLINOU a pour objectif d’aider les enfants à développer leurs compétences dans le contexte de la classe. En s’appuyant sur les programmes de l’école maternelle, cette application propose vingt activités différentes permettant aux élèves de moyenne et de grande section de maternelle de développer leurs compétences en littératie émergente (c’est-à-dire, connaissance des lettres, conscience phonologique et langage oral) et en numératie émergente (c’est-à-dire, connaissance des chiffres, dénombrement, cardinalité, sériation, …).

Des univers graphiques variés sont présents pour chaque activité, permettant ainsi à l’enfant de se repérer plus facilement dans l’application. De même, l’interactivité de l’outil (consignes orales, bouton de réécoute de la consigne, bouton de validation) permet aux élèves d’être autonomes durant l’activité tout en bénéficiant de feedbacks visuels et auditifs spécifiques selon leurs besoins leurs permettant de progresser dans l’activité.

Afin d’évaluer l’efficacité de cette application, une méthodologie expérimentale et longitudinale a été utilisée. Durant trois années, une cohorte d’élèves scolarisés initialement en moyenne section a été suivie et évaluée afin de mesurer l’efficacité du dispositif mis en place. Plus de la moitié des élèves de cette cohorte (groupe expérimental) ont utilisé l’application AppLINOU à hauteur d’une vingtaine de minutes par semaine en moyenne section (durant 10 semaines) et d’une trentaine de minutes par semaine en grande section (durant 15 semaines). Par ailleurs, les évaluations nationales de début CP ont été récupérées afin de comparer les élèves du groupe expérimental et ceux du groupe contrôle avec l’échantillon national.

Les premiers résultats montrent qu’une plus faible proportion d’élèves du groupe expérimental (en comparaison de ceux du groupe contrôle et de l’échantillon national) est considérée comme rencontrant des difficultés importantes en français et en mathématiques. De même, un pourcentage plus important d’élèves du groupe expérimental a une bonne maitrise des compétences évaluées dans les domaines évalués en comparaison avec ceux du groupe contrôle et de l’échantillon national. De plus, des analyses de régression multiniveaux ont montré que l’intervention a eu un impact positif sur la progression des élèves du groupe expérimental en début CP. Toute chose égale par ailleurs, ces élèves progressent significativement plus que les élèves du groupe contrôle aussi bien en français qu’en mathématiques.

Photo d'enfants qui utilisent le logiciel AppLinou
Photo d'enfants qui utilisent le logiciel AppLinou

Disponibilité

L’application AppLINOU a été conçue pour être utilisée par des enseignants et des élèves de moyenne et grande section de maternelle. Actuellement, elle n’est pas disponible pour de libres utilisations en classe, son usage étant exclusivement réservé à la recherche. À terme, elle sera proposée en téléchargement via ce site et les stores Androïd et iOS.

En savoir plus

Liberté Égalité Fraternité

Cette plateforme e-FRAN vous informe sur les résultats de travaux de recherche qui font très largement écho à des pratiques d’éducation, d’enseignement et d’apprentissage, elles-mêmes susceptibles d’être sources d’innovations pédagogiques.
Elle est éditée par le Ministère de l'Éducation Nationale et de la Jeunesse et par le Ministère de l'Enseignement Supérieur et de la Recherche, et réalisée en partenariat avec des laboratoires engagés dans le cadre de la mission sur le numérique dans l'éducation.

service-public.fr

gouvernement.fr

education.gouv.fr

enseignementsup-recherche.gouv.fr

Sauf mention contraire, tous les textes de ce site sont sous licence etalab-2.0

©2023 e-FRAN